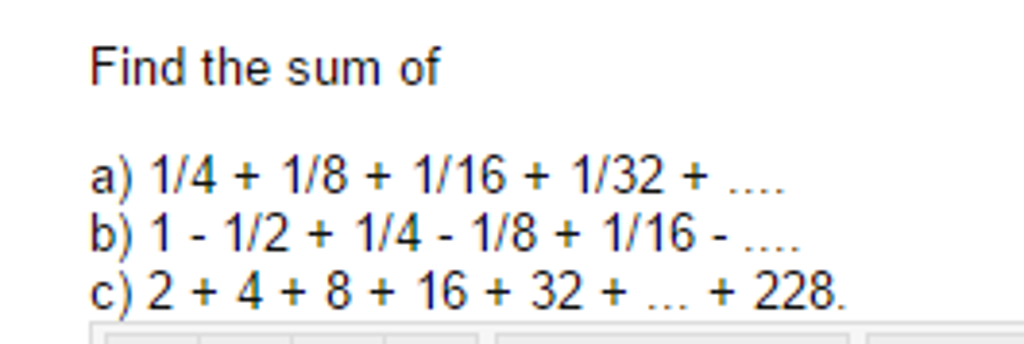1 2 1 4 1 8 Series

In this case multiplying the previous term in the sequence by gives the next term.

1 2 1 4 1 8 series. Say a 1 2 1 4 1 8. So a a 1 2 1 2 since all the other terms will cancel. This is the form of a geometric sequence. Then a 1 2 1 4 1 8 1 16.

All cancel and we get s 1 2 s 1 which means s 2 1 and so s 2. Identify the sequence 1 2 1 4 1 8 1 16 this is a geometric sequence since there is a common ratio between each term. It was used by archimedes circa 250 200 bc. In this video we see some examples introduce the terminology and then give the formal definition o.

C program to print sum of series 1 1 2 1 4 1 8 1 n here we have listed how to print the sum of series of numbers in the format 1 1 2 1 4 1 8 1 n in c programming language. It is important that we should know about the how a for loop works before getting further with the c program code. Now if we subtract the second equation from the first the 1 2 1 4 1 8 etc. The euler transform of the divergent series 1 2 4 8 is 1 2 1 4 1 8 1 16.

In other words. There are many different expressions that can be shown to be equivalent to the problem such as the form. Okay what you need to do is change the way you look at it. 3 challenging mathematical riddles.

This same technique can be used to find the sum of any geometric series that it a series where each term is some number r times the previous term. Dalam matematika deret tak hingga 1 2 1 4 1 8 1 16 adalah contoh dasar dari deret geometri yang konvergen absolut. A series is the infinite sum of the terms of a sequence. In mathematics the infinite series 1 2 1 4 1 8 1 16 is an elementary example of a geometric series that converges absolutely.