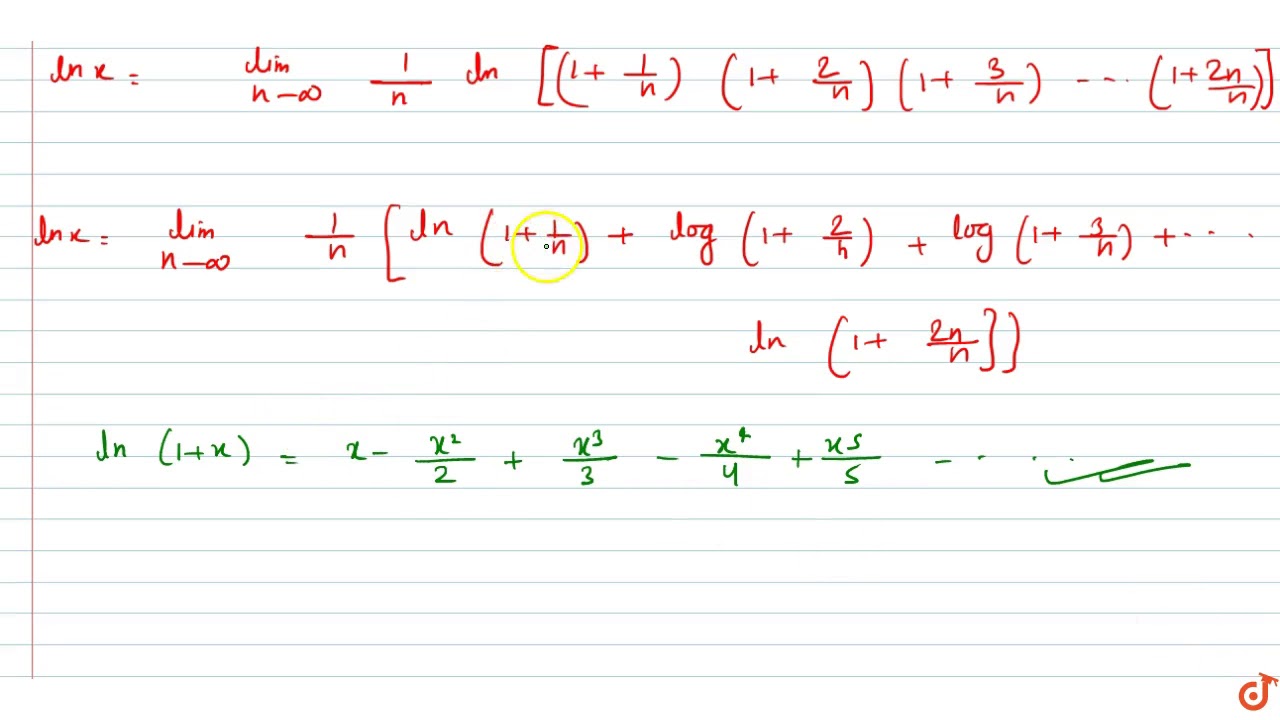1 2 1 4 1 8 Dots N 1 2n 1 1 2 N

Prove the following by using the principle of mathematical induction for all n n.

1 2 1 4 1 8 dots n 1 2n 1 1 2 n. 1 2 1 4 1 8 1 2𝑛 1 1 2𝑛 let p n. 1 2 1 4 1 8 1 2𝑛 1 1 2𝑛 for n 1 we have l h s 1 2 r h s 1 1 21 1 2 hence l h s. A monotonic path is one which starts in the lower left corner finishes in the upper right corner and consists entirely of edges pointing rightwards or upwards. There are many different expressions that can be shown to be equivalent to the problem such as the form.

Rule is x n x n 1 x n 2 that rule is interesting because it depends on the values of the previous two terms. Rules like that are called recursive formulas. N n 1 2 1 3 6 10 15 clearly the required sequence is double the one we have found the nth term for therefore the nth term of the required sequence is 2n n 1 2 n n 1. 2 1 2 2 2 3.

C n is the number of monotonic lattice paths along the edges of a grid with n n square cells which do not pass above the diagonal. In mathematics the infinite series 1 2 1 4 1 8 1 16 is an elementary example of a geometric series that converges absolutely.