1 1 2 3 5 8 Pattern

C program to print pyramids and patterns in this example you will learn to print half pyramids inverted pyramids full pyramids inverted full pyramids pascal s triangle and floyd s triangle in c programming. In the first pattern 3 is added. 4 2 2 2 2 1 1 2 1 2 1 2 2 1 4 1 4 2 1 8 and so on.

5 causas de la independencia de las 13 colonias de norteamérica 5 1 2 x 8 1 2 binder 4k ultra hd call of duty mobile wallpaper pc 4g lte sim card router 4k portrait ultra hd game of thrones wallpaper 4k 5 1 next to 6 0 4k ultra hd call of duty pc wallpaper 4g wifi router with sim card slot

What Is The Pattern Of Sequence 1 1 2 3 5 8 13 Quora

Number Series And Puzzles Tricks And Solutions 1 1 2 3 5 8 13 Youtube

Https Encrypted Tbn0 Gstatic Com Images Q Tbn 3aand9gcttknk66fhx Bgym1ipo30agmadbg5xoayscq Usqp Cau

Fibonacci S Rainbow Dreamhouse Album On Imgur

The Fibonacci Sequence Nanotedsla

The pattern is continued by multiplying by 2 each time like this.

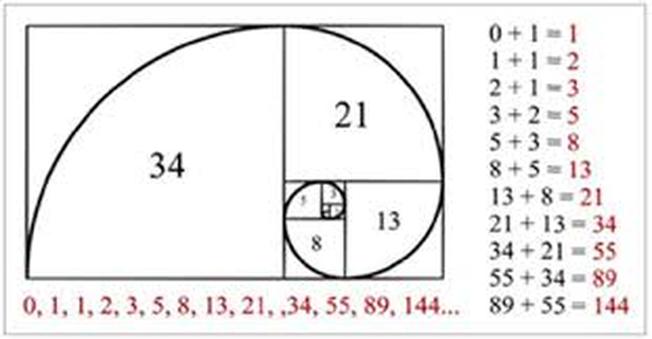
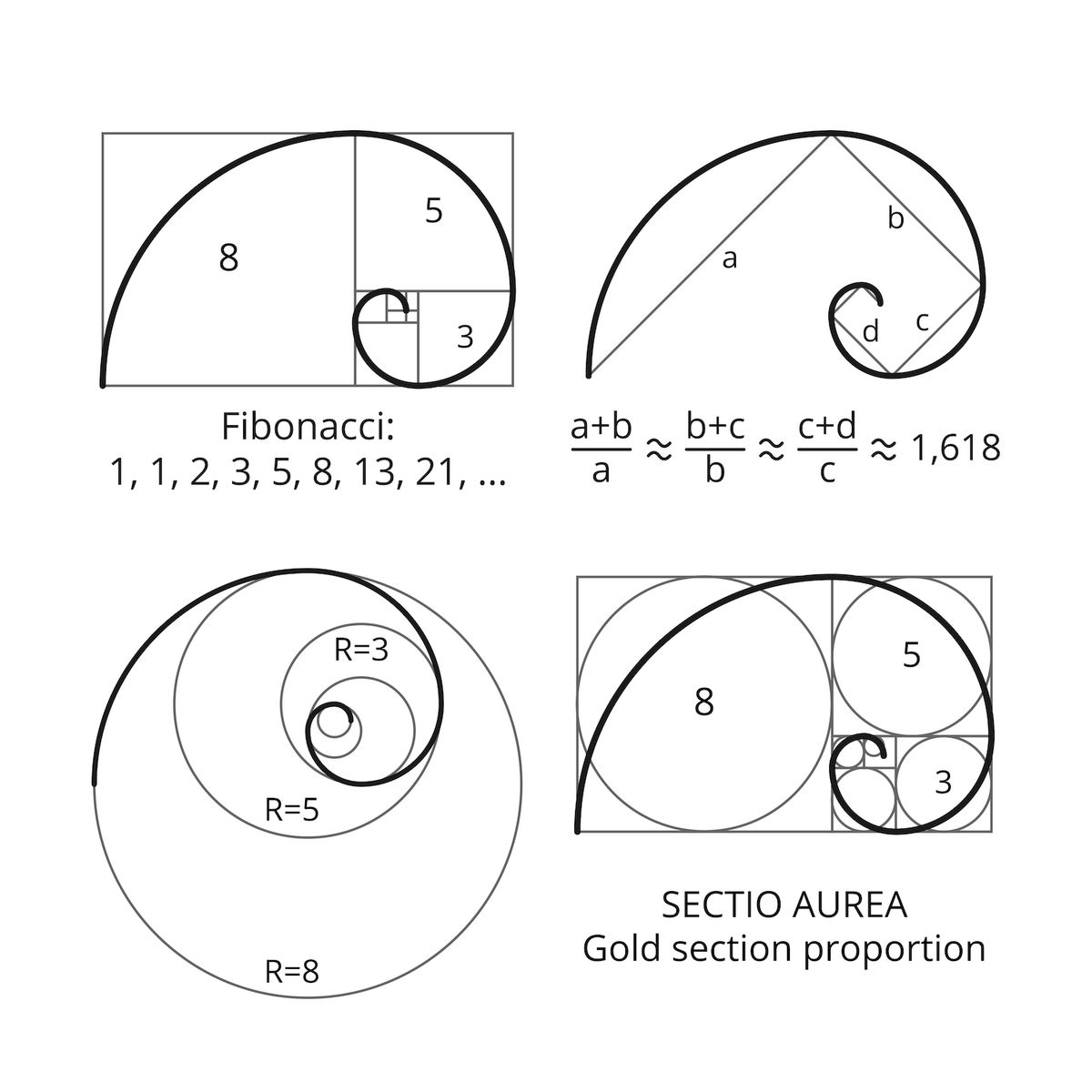
1 1 2 3 5 8 pattern. To illustrate this consider the following sequence of numbers 1 3 5 7 9. In the second 2 is subtracted. Multiply the previous number by 2 to get the next one the dots at the end simply mean that the sequence can go on forever. We can make another picture showing the fibonacci numbers 1 1 2 3 5 8 13 21.

If we start with two small squares of size 1 next to each other. 0 1 1 2 3 5 8 13 21 34. Clearly the first term of this number pattern is 1. 0 1 1 2 3 5 8 13 21 34 55 89.

On top of both of these draw a square of size 2 1 1. In the present form of the gleason system prostate cancer of gleason patterns 1 and 2 are rarely seen. When referring to sequences like this in mathematics we often represent every term by a special variable. View answer discuss in forum workspace report.

And then another touching both the 2 square and the 3 square which has. The fibonacci sequence is the series of numbers. There are often just sheets of cells throughout the surrounding tissue. This is a simple alternating addition and subtraction series.

Gleason pattern 3 is by far the most common. Pattern 5 the tissue does not have any or only a few recognizable glands. The common ratio can be less than 1. This corresponds to an anaplastic carcinoma.

Look at this series. The fibonacci sequence is the series of integers. Each element in the series is the sum of the. Find more mathematics widgets in wolfram alpha.

36 34 30 28. Report errors view. 10 5 2 5 1 25 0 625. X 1 x 2 x 3 x 4 x 5 x 6 x 7.

Get the free pattern finder widget for your website blog wordpress blogger or igoogle. This sequence starts at 1 and has a common ratio of 2. We can often describe number patterns in more than one way. The next number is found by adding up the two numbers before it.

1 2 2 4 2 8 2 16 2 2 2 pattern. We can now draw a new square touching both a unit square and the latest square of side 2 so having sides 3 units long. And the terms after the first term are obtained by adding 2 to the previous term.