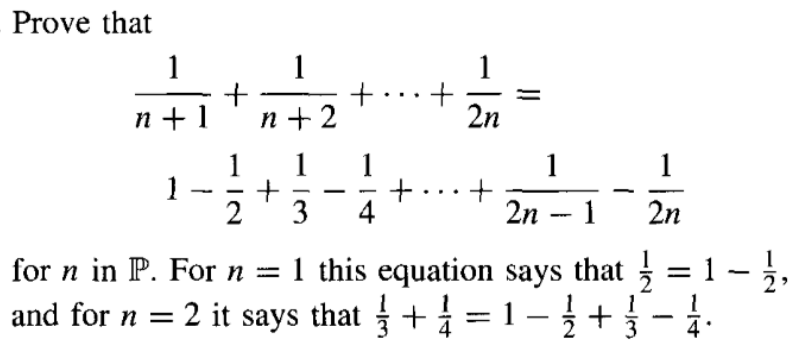1 1 2 1 3 1 N Formula

I can give you a good approximation if you would prefer. Math central is supported by the university of regina and the pacific institute for the mathematical sciences. How to find 9th n for the below formula h n r 1 1 r 1 2 r 1 n r.

0 1 3 6 10 formula 1 1 1 2 054 تبع اي شركة 0022 مفتاح اي دولة 0 3 month baby boy halloween costumes 0 6 1 5 adalah 0 6 dibagi 1 5 1 1 1 day

Ex 4 1 11 Prove 1 1 2 3 1 2 3 4 1 3 4 5 1 N N 1 N 2

Understanding The Proof That The Series Sum Frac 1 N 2 Is Convergent Mathematics Stack Exchange

Solved Prove That 1 N 1 1 N 2 1 2n 1 1 Chegg Com

Pdf Important Sum Formulas Omid Motahed Academia Edu

Rancang Formula Yang Memenuhi Setiap Pola Berikut Ini Brainly Co Id

$Harmonic Series Mathematics Wikipedia$

Harmonic Series Mathematics Wikipedia

The number h n 1 1 2 1 3 1 n is a rational number.

1 1 2 1 3 1 n formula. Its name derives from the concept of overtones or harmonics in music. Sum of the reciprocals sum r 1 n 1 r h n where h n is the nth harmonic number. Sum of the reciprocals of the squares sum r 1 n 1 r 2 pi 2 6 sum r 1 n beta k n 1 k where beta x y is the beta function. In mathematics the harmonic series is the divergent infinite series.

Is there any formula for this series 1 1 2 1 3 1 n i think it is a harmonic number in a form of sum 1 k for k 1 to n. What is your question konrad. Program to find sum of the series 1 3 3 5. The denominator goes from 1 to n.

1 1 1 2 1 3 1 4. The wavelengths of the overtones of a vibrating string are 1 2 1 3 1 4 etc of the string s fundamental wavelength every term of the series after the first is the harmonic mean of the neighboring terms. Program to find the sum of the series 1 a 2 a 2 3 a 3 n a n. Ln n 1 le sum i 1 n frac1i le ln n 1 this is a rather tight upper limit and lower limit you can use to approximate your answer.

Well whats the pattern. Summation i 1 n and 1 n. So you have a summation problem. I won t go into a full explanation as it too complex.

Program to find length of bridge using speed and length of train. Do you want to calculate h n in lowest terms with finite number of operations or just any representations of h n.